正交多项式法拟合密度函数

正交多项式法拟合密度函数

连续型随机变量的概率密度函数可用高阶矩的展开式逼近，而且展开式为正态分布乘一修正系数，所以可以展开为带权的多项式。下面给出利用样本的前阶矩近似拟合密度函数的过程。本文取l=6，即利用失效参数样本的前6阶矩近似拟合参数的条件密度函数。

选取区间上的正交多项式

作为概率密度拟合的基函数，其中表示第k项多项式中x的m次幂项的系数，当上述正交多项式基的类型选定后，其系数即可确定。例如，本文选取埃尔米特正交多项式作为基函数来拟合条件密度函数，其前7项分别为

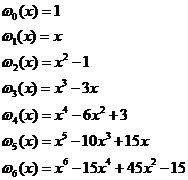
则=1；=0、=1；=-1、=0、=1；=0、=-3、=0、=1；由正交多项式的性质有

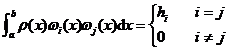
其中权函数的选取将根据选用的正交多项式类型的不同而不同。若选用埃尔米特正交多项式作为基函数，则权函数取为下面的形式

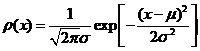
其中、分别为总体均值和标准差。经函数标准化之后，权函数可取为

而为确定常数，当选定正交多项式基的类型后，即可由式的积分确定。文中选定埃尔米特多项式作为基函数时，容易确定。

用带权的正交多项式逼近失效样本的概率密度函数函数为

上式中为待定系数，可由式确定。

其中为样本的m阶中心矩。

将拟合得到的失效参数样本的条件密度函数(式所示)及8.1节中确定的、代入式即可求得失效概率函数。

分别按照上述的自适应核密度估计法和正交多项式法的步骤拟合得到失效概率函数后由式所示的全局灵敏度求解公式即可进行全局灵敏度的求解。